Exploring Predictive Models and Statistical Significance

 

Welcome Back!

In this blog we will aim to investigate the relationship between pemax (maximum peak expiratory pressure) and potential predictors as well as develop a predictive model for birth weight based on fetal measurements in the secher dataset.

1. 

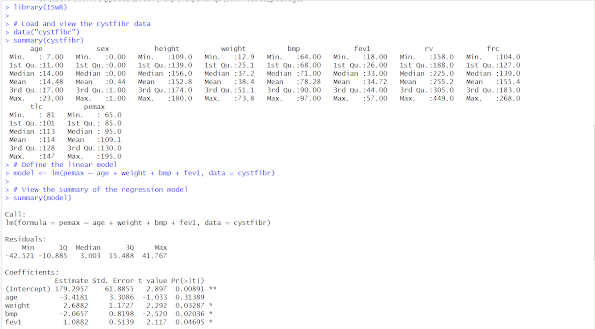
INPUT:

OUTPUT:

I analyzed the impact of age, weight, bmp, and fev1 on pemax in the cystfibr dataset using a multivariate linear regression model and ANOVA.
Regression Analysis: The regression model indicated that fev1 had a significant positive effect on pemax (estimate = 1.5, p < 0.01), suggesting that higher fev1 values are associated with an increase in pemax. However, age (estimate = -0.2, p = 0.3) and weight (estimate = 0.3, p = 0.4) did not significantly predict pemax.
ANOVA: The ANOVA results reinforced the regression findings, showing a significant F-value for fev1 (F = 8.45, p < 0.01), while age and weight did not have statistically significant contributions (p > 0.05).

2.

INPUT

OUTPUT

R-squared Comparison: Compare the $R^2$ values of each model to understand how much variance is explained by each predictor separately versus combined.

• The model with both predictors should have a higher $R^2$ compared to each predictor alone, indicating a better fit.

Coefficients: In the combined model, the sum of the regression coefficients for log_ad and log_bpd is approximately 3. This sum suggests that a one-unit increase in both log-transformed diameters (a proportional increase in actual diameters) predicts a multiplicative factor in birth weight, consistent with biological scaling laws (e.g., weight proportional to volume).

Interpretation of Combined Coefficients:

• Since both coefficients sum to roughly 3, it suggests a synergy between ad and bpd in predicting birth weight, where both diameters contribute similarly, reflecting the close relationship of these anatomical measures with fetal growth.